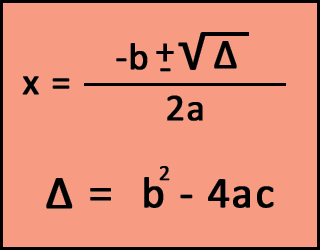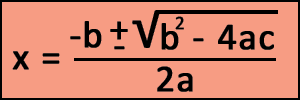How to Solve a Quadratic Equation?
Let's take some examples to understand the process step by step.
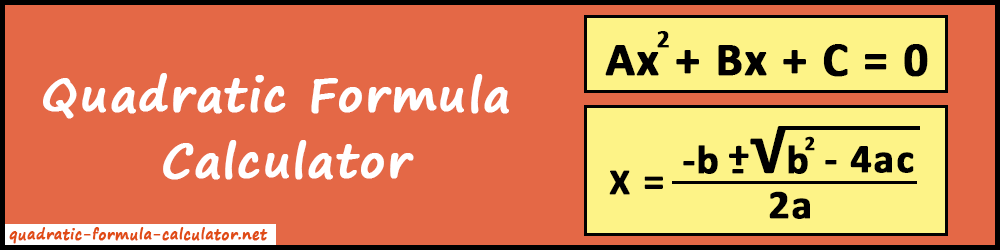
Example 1: Solve 2x2 + 5x = -3
Firstly, convert the equation into a standard form like this: ax2 + bx + c = 0.
Take -3 from right to left-hand side. As a result, we get:
2x2 + 5x + 3 = 0
So, we have:
Now place the known values in the quadratic formula.
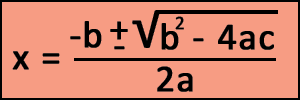
| x = |
| -5 ± √(52) - 4(2 × 3) | | | 2 × 2 |
|
As you can see, the discriminant (b2 - 4ac) = 1 that is > 0. So, there are two real roots.
For the First Root:
For the Second Root:
So, the roots of 2x2 + 5x + 3 = 0 are -1 and -1.5.
Example 2: Solve 4x2 + 15x + 20 = 0
Here Coefficients are:
Firstly, let's find the discriminant (Δ):
Δ = b2 − 4ac
= 152 - 4 × (4 × 20)
= 152 - 4 × (80)
= 225 - 320 = -95
Here, the discriminant is -95. That is negative. So, we will get 2 complex roots.
Now let's find the roots.
√(-95) = 1.21835i ( Where i = √−1, Imaginary number )
Finally, the First Root = -1.875 + 1.21835i and the Second Root = -1.875 - 1.21835i
To solve complex quadratic problems with ease, use our quadratic formula calculator. It will make your calculation easier, faster, and more accurate.